본 게시물은 이석복 교수님의 네트워크 강의를 수강하며 작성한 강의노트와 추가 공부한 내용을 바탕으로 작성하였습니다.
- 참고 강의 및 사이트
KOCW
한양대학교 이석복 강의 내용 및 목표 인터넷을 동작시키는 컴퓨터네트워크 프로토폴을 학습한다. 주제분야 공학 >컴퓨터ㆍ통신 >컴퓨터공학 강의학기 2015년 2학기 수강 확인증 발급 안내 수강
www.kocw.net
https://choiblack.tistory.com/33
[Network] Routing algorithms - Distance Vector
이 포스팅은 앞선 Routing Protocols - link state 다음으로 이어진다. 라우팅 알고리즘의 목적 라우팅 알고리즘의 목적은 출발지 라우터에서 목적지 라우터까지 최단 비용으로 갈 수 있는 길을 찾는 것
choiblack.tistory.com
Routing Algorithm
라우터가 포워딩 테이블을 어떻게 형성하는지 그 방법에 대한 것이다.
이제부터 네트워크를 그래프로 살펴보면 네트워크의 구성요소는 그래프에서 다음과 같이 연결해 생각해볼 수 있다.
node : router edge : link value : link cost(거리 또는 트래픽 양)
라우팅 알고리즘엔 크게 두가지 방식이 존재한다. 첫번재는 모든 라우터가 전체적인 비용에 대한 그림을 가지고 있다는 전제로 계산하는 경우인 ‘Link State’이며 두번째는 전체 그림은 없과 이웃과 정보를 교환해서 최단 경로를 구하는 방법인 ‘Distance Vector Algorithm’이다.
각각 어떤 과정으로 포워드 테이블을 구성하는지 살펴보자.
Link State
모든 라우터의 정보를 알고 있을 경우에 사용한다. 흔히 알고 있는 다익스트라 알고리즘과 동일하다.
다익스트라 알고리즘 포스팅으로 설명을 대체한다.
(알고리즘) 다익스트라 (JAVA , for문 활용 & PriorityQueue 활용 방식 비교)
1) 개념 한 정점(노드)에서 다른 정점(노드)까지의 최단 경로를 구하는 알고리즘 도착 정점 뿐만 아니라 다른 정점까지 최단경로로 방문하여 각 정점까지의 최단 경로를 모두 찾을 수 있음 탐욕
the-square-of-y.tistory.com
Distance Vector Algorithm
이웃들과의 자료교환으로 계산한다. 따라서 포워딩 테이블이 갱신될 때마다 이웃들에게 갱신된 정보를 또 전달하여 포워딩 테이블을 구성한다.
노드들은 이웃으로부터 새로운 값을 전달받으면 해당 값을 이용해 자신의 테이블을 재갱신하며 이 때 갱신되는 값이 있다면 마찬가지로 또 다시 해당 정보를 이웃에게 전달한다.
위 과정을 더이상 갱신되는 값이 없을 때까지 반복한다.
따라서 Distance Vector 알고리즘은 아래와 같은 특징을 갖는다.
- 분산적(Distributed) : 각 노드는 직접 연결된 이웃 노드들로부터 정보를 받고 계산을 수행하며 해당 결과를 다시 인접 노드들에게 배포한다.
- 반복적(Iterative) : 이웃끼리 더 이상 정보를 교환하지 않을 때까지 프로세스가 반복된다.
- 비동기적(asynchronous) : 톱니바퀴가 돌듯 모든 노드가 정확히 맞물려 동작할 필요가 없다.
알고리즘 과정
Distance Vector Algorithm은 아래와 같은 식으로 포워딩 테이블을 갱신해간다.

아래 사진의 예제를 통해 자세한 방법을 단계적으로 살펴보자.

y로 인해 z값이 갱신되는 상황을 단편적인 예로 고려해보면, node y로부터 전달받은 값을 통해 D_x(z)의 값이 갱신됐으며 이를 또 이웃 노드들에게 전달하여 D_y(x)의 값이 갱신된다.
Poisoned Reverse
이렇게 새로 갱신되는 값이 기존의 값보다 적은 비용일 경우는 큰 문제는 발생하지 않으나 큰 비용으로 갱신되는 경우 ‘poisoned reverse’가 발생할 수 있다. 최소경로가 되돌아가는 경로를 포함하는 값일 경우 역류하는 경우이다. 이를 대비하여 온 길은 무한대로 업데이트하여 역류를 방지한다.
위 상황을 설명하는 자세한 예제를 보자.
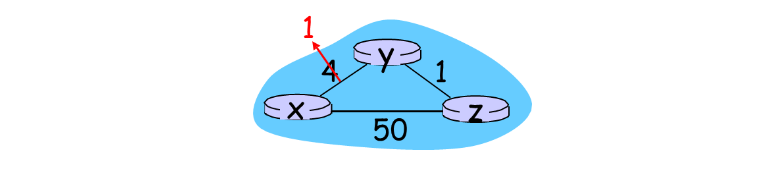
위 사진과 같이 라우터 링크 비용이 4에서 1로 감소하는 경우를 살펴보자.
y 테이블은 x와의 비용 값을 수정하고 이를 x와 z에게 전달할 것이다. 아래는 전달하여 z테이블이 테이블을 갱신하는 과정을 보여준다.
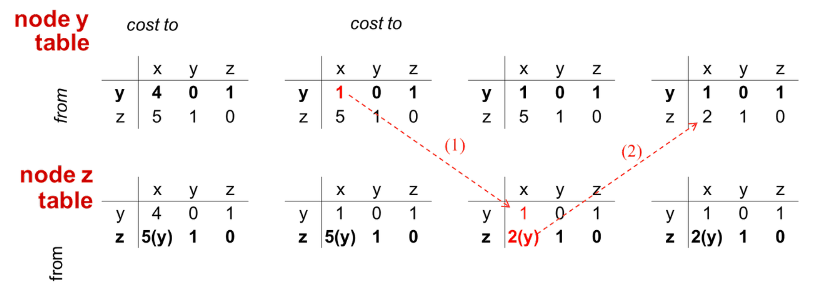
이렇게 비용이 감소하는 경우는 빠르게 감소된 비용으로 갱신될 수 있음을 알 수 있다.
비용이 증가하는 경우는 어떻게 테이블이 갱신될까?
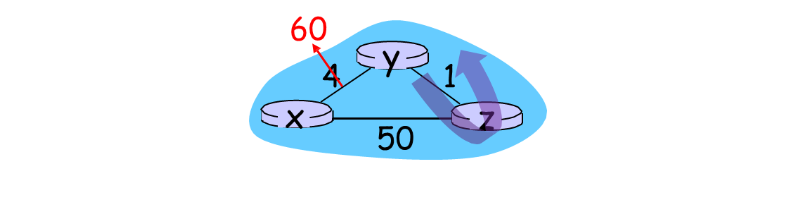
위 사진과 같이 x와 y를 연결하는 링크의 비용이 4에서 60으로 증가한다고 가정하자.
비용이 감소했을 때와 마찬가지로 y테이블은 이웃들에게 변경된 값을 전달할 것이다. z는 이 값을 받아 테이블을 수정하고 이웃인 x,y테이블에게 갱신된 값을 전달하게 된다.
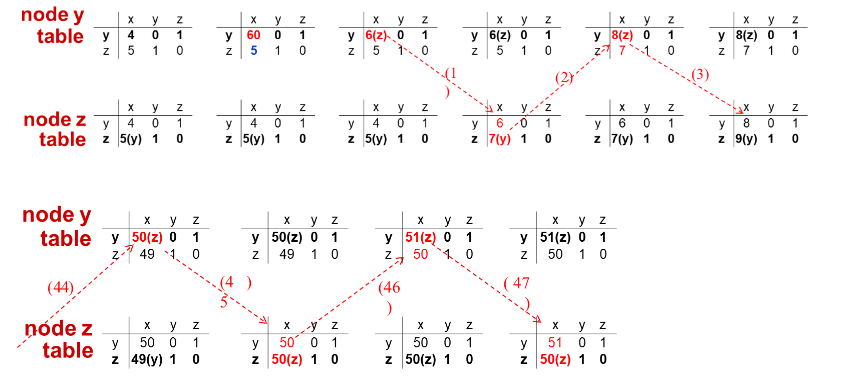
전자의 상황과 달리 상당히 많은 과정의 테이블 갱신이 이루어짐을 한 눈에 볼 수 있다.
y테이블의 변화를 받은 z는 D_z(x) = min(D_z(x), D_z(y)+cost(y,x))를 수행하여 증가한 cost보다 작은 자기 자신의 값을 유지하게 되며 y는 이렇게 유지된 값으로 다시 D_y(x)값을 D_y(z)+cost(z,x)로 갱신하여 6이 된다. 이렇게 처음에 z테이블의 값이 유지되면서 D_y(x)값이 1씩만 증가하여 테이블이 안정되지 않고 계속 위 사진과 같이 많은 반복이 발생한다.
근본적인 원인은 처음 z테이블이 갱신될 때 D_z(x)값이 y를 거쳐가는 경로 값이었다는 것이다. 증가하기 전의 cost(x,y)를 사용함으로써 계산된 값을 비용이 증가한 이후에도 그대로 사용해서 생긴 문제이다.
이러한 문제를 “Count to infinity problem” 이라고 한다. 따라서 최소 경로를 계산할 때 결정적인 역할을 한, 즉 거쳐온 이웃 라우터에게 경로 비용을 무한대로 전달하는 “Poisioned Reverse”를 사용하여 이러한 문제를 해결한다.
'Learning-log -CS > Network' 카테고리의 다른 글
| (컴퓨터와 네트워크 / 이석복) 무선이동네트워크 (IEEE 802.11, LAN, AP, BSS, CSMA/CA, RTS, CTS, Frame, SNR) (1) | 2024.03.01 |
|---|---|
| (컴퓨터와 네트워크) 링크 계층(CSMA, CSMA/CD, Ethernet, ARP, 스위치) (1) | 2024.02.28 |
| (컴퓨터와 네트워크) 네트워크 계층(IP, DHCP, ICMP) (1) | 2024.02.15 |
| (컴퓨터와 네트워크) TCP (특징, 구조, 흐름제어, 혼잡제어) (1) | 2024.01.23 |
| (컴퓨터와 네트워크) 전송 계층 (기능, UDP, RDT의 원리) (1) | 2024.01.22 |



